主题：我又来说掏心窝子的话了 -- 给我打钱87405

就从一道中学物理题开始吧，原题见下图：

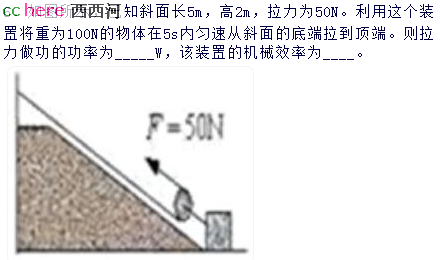
有两种解法。

一种是：原先（这个原先是自己创造 出来的，这一点尤其需要学生体会）是垂直提升5米，现在沿斜面运动5米，显然原先的效率要高一些（注意这里的效率其实只考虑了势能，题目并不严谨）。

另一种是：原先垂直2米，也只沿“垂直面”运动了2米。现在还是垂直2米，但沿的斜面运动了5米。显然也能看出来后者效率低。

要注意这里容易出现的一个“陷阱”，就是学生往往习惯了从力的角度去分析问题，而这里是直接从功或者说能这个角度切入。这实际上是在考察学生选择“工具”的能力。

这是第一大步。

下面要进入到第二大步。

不论学生之前如何，经过这一大步，学生会产生一个意识：变。

我以为，老师真正要教会学生的就是变。变到底指的是什么呢？具体而言，就是改变一个或多个相关要素，也就是改变条件。条件改变，结果就有可能发生变化。简化来说，输入变了，输出就有可能变。

可是，站在学生的角度，他们可能还不习惯这种思考方式，他们往往是看到什么就思考什么，而不会“自己找一些东西”来做比对——这种方法，本质上是一种进阶式的“组合法”。

任何一门学科里的问题，都可以拆分成最基本问题（当成夸克好了）的组合。但是我们在解决问题时，并不总是需要从最基本问题开始，而是可以找一个与现有问题比较接近的模型，把这个模型当成基本型。这模型之所以可以成为基本型，是因为“我知道它是怎么回事”。

好比几何中有一些进阶公式，它们实际上并非是公理，而是定理，但是解几何题时，却可以直接调用这些进阶的定理，与我前面说的，就是同一个道理了。简而言之，我们不必非要从零开始，既可以说，2比0多2，也可以说2比1多1。所以还要教会学生会根据具体情况来进行选择，选择谁成为基本型。

但是我们仍然要注意，把一个相对简单的综合问题当成基本型，是为了解决问题，而不是为了理解问题。这是第三大步要涉及的教学内容。

在学习的初期尤其要注意一点，否则学生很容易沉迷于掌握解题的技巧。这也是为什么要补上“自己出题、变题”这一环节的原因。

就拿此题来说，找基本型时，把“沿着垂直方向运动5米”和“沿着斜面运动5米”作为一个对比组，这一点容易想到吗？

那么另一个对比组呢？“垂直提升2米”和“沿着斜面上升2米”为什么更容易想到呢？

是不是因为我们在前面讲过“斜面省力”这一知识点呢？

为什么我们会不断的讲“斜面省力”呢？是不是因为我们首先锁定了输出结果呢？也就是“垂直提升2米”这个结果是不变的呢？

那么我们在这之前，有讨论过“垂直运动5米”跟“沿斜面运动5米”在输出上的不同吗？

在这里就很容易看出来人的一种思维习惯：先锁定目标，反推怎么做，可以怎么做。

这种思维习惯真的是万能的吗？

我们是否需要另一种思维：从“怎么做”到“会有什么结果”呢？

如果我把这个问题拓展开来讲，你就会发现它影响的是方方面面。

比如我们一些家长在培养孩子时，往往只会反推法：我要进一个大牌企业——所以我只能就读大牌高校——所以我只能就读大牌中学——所以我只能就读大牌小学——所以我只能就读大牌幼儿园——所以我只能出生于大牌妈咪的肚子，配上大牌爹地的精子——所以我只能出生于富豪世家。

但由于我并非出生于富豪世家，所以我最终无法进入大牌企业，所以我的人生在出生时就已经结束了。

这一所谓的“矛盾体”不光出现在物理中，在其它学科，比如语文、数学中也屡见不鲜。好比作文，既有反推写作法，也有顺势写作法，这些学生注意到了吗？那么几何证明题呢？是不是往往只注意到了反推法呢？

思维只有一条腿，真的很好吗？难道我们不应该学会两条腿走路吗？我以为，就不必再论证两种思维我们都是需要的了。可是我们如何调和它呢？

我们不是牛顿，似乎只能从前人那里学到“斜面省力”的知识，但是我们学到这个知识之后，我们是否可以这么去思考问题：

同样的运动距离，一个垂直，一个沿斜面，这二者必然是有不同的。这是完全可以“拍脑子”做出的一种比较合理的推理或者说猜想。

那么我们把自己的脑袋放空，去做进一步的猜想。如果把垂直当原型，那么变成了斜面之后，得到了什么？又失去了什么呢？

是不是很容易看出来，“失去了”一部分高度呢？这些“失去的高度”去了哪呢？

我们大概就能猜想出来（如果能结合 实际感受则更好），“失去的高度”与“多余的力”是等价的，是一个硬币的两个面。

而既然有“多余的力”，那么就意味着可以减力，这样也能得出“斜面省力”的结论。

我在这里，实际上就是换了一条腿走路。

我们经常讲，学习不能是拿来主义，但我们又不可避免的要拿来，那么我们究竟怎么做，才能实现不简单的拿来呢？我以为，我举的这些个例子，这里面所包含的方法、思想，是可以广泛应用的。

还是以这道题为例。

当我们谈效率时，谈的是什么效率？真的很全面吗？为什么要说一些功是无用功？

实际上，经过研究分析就会发现，这种无用功的假定，是人设的。我们完全可以分析出来，功，有没有用，更取决于人的看法。当人找不到如何利用它时，便说它无用，这恰好就是偏见的来源。

事实上，斜面运动中，一部分功转换成了热能（摩擦发热）和动能（斜面拉得快）。

而进一步分析，就可以知道，垂直运动中功与能的转换，是功100%转换成了势能，水平运动中，是功100%转换成了热能，斜面居中（当然这里没有考虑动能）。

这样我们看问题是不是就更全面了呢？

从一道简单的物理题中，经过“一菜三吃”，能得到这么多东西，既讨论了一些具体的物理问题，又从中得到了一些启发，拓展了自己的思维方向，体会到了挖掘价值、价值实现的重大意义，最终的收获又岂止是一菜三吃呢？

所以说，世界本来是很大的，自己弄小了，那是自己的问题。

同时，我想我也向大家提供了一种新的路径：如何在另一个层面实现“因材施教”。大家学的是同一道物理题，有的学生从中汲取了物理知识，有的学生却能领悟到一些哲学思想。

我们以前谈因材施教，往往是指，甲生是学数学的料，乙生是学历史的料，所以给甲生喂数学题，给乙生喂历史题。

那么我这种方法，很少被注意到，至少可以说现在是非主流。我给甲、乙两名学生喂一道题，拖来同一只猪，一个吃腿，一个食肚，各取所需，这难道不可取吗？

所以我提倡的学习方法是，至少要一菜两吃。在自然学科 中要带着人文，在人文学科中不妨带上自然。

===========================

可以再举一个例子。

我女儿最近在读一本书，叫《最动人的世界史》。这本书的第二章，谈的是生命的起源。在此章的第二部分，谈到了一个问题：创造内部。

书中写到，蛋白质由两类氨基酸组成，一种是亲水的，另一类是疏水的，二者如何“抱团组队求生存呢？”亲水的在外面，疏水的在里面，形成了一个闭合的结构。这样，就创造出了“内部”。在这里，产生出“内部”后，就出现了“外部”。

读到此处，我就向孩子讲解我的一些理解。

比如，当我们说“一袋子鸭脖”的时候，指的是什么呢？包含这袋子吗？不包含，袋子是第三方，是将鸭脖与“其它”隔离的一道“墙”。

可是，当我们说城墙的时候，城墙是城的一部分吗？显然，城墙是城的一部分。

一张白纸，我们无法感受到内部和外部，但是当我们在这白纸上画一个圆之后，我们马上就能产生内外部的看法。可是，这个圆周，在我们的意识中，到底是圆的一部分，还是装鸭脖的袋子呢？

“这个问题以前困扰了我很久！”女儿马上说，“一方面，我认为圆周像袋子，不是圆的一部分，但是另一方面，似乎圆周就是圆的一部分。今天我终于明白了。”

进一步，我向女儿重申了以前的一个问题：宇宙到底有没有边缘？

以前的推理是：如果宇宙有边缘——那么宇宙之外一定还有什么——这就跟“宇宙就是一切”的定义相冲突了。现在来看，这个推理有很大的毛病。有边缘，一定就有内、外部吗？

所以，经过讨论，就有了这样的看法：内、外，是一个空间概念。而边缘，是一个成份概念。这是两个概念。但由于这两个概念往往同时出现，人们很容易将它们混为一谈。而像这样的案例，可谓数不胜数。比如，在讨论力的问题时，往往会把方向与大小混为一谈。当然，我们实际上是把二者合并了。同样大的推力，垂直作用我们感受到施力最大，斜向作用感受到施力变小了。这里面其实是有一个方向概念的，但是很多学生往往忘了这一点。

另外还注意到一个问题，就是我们的汉语，在讲内部和外部时，是两种概念混用。比如当我们谈自己人、别人、内部问题和外部问题时，其实讲的是一个成份概念。但是在另一些情况下，我们又讲的是空间，比如城里、城外。

这样我们就意识到，读书时，并不能望文生义，要结合具体的语境来分析，同样一句话，在不同的环境 中，究竟各自指的是什么。这就“证明”了，读书是要动脑子的。

就这么一段文字，这么一个知识，作为老师，我引导孩子做了范围的“跨界思考”，这是因为我认为，对于许多人来说，知道不知道蛋白质的空间结构，并不会影响生活质量，但是不知道内、外问题，恐怕就是大问题了。

===================================

那么可能就会有人提问：你这是“一菜多吃”，我的是“吃多菜”，如果你是“多菜多吃”，那么学得过来吗？

对，这是一个问题，所以我们意识到，这里面有一个度的问题。我们必然要“一菜多吃”与“吃多菜”之间做一个选择，找一个点。

而显然，在目前的教育框架之下，“一菜多吃”这种主观性很强的教学方法，是很难大面积推广的。学校主要是靠“吃多菜”，甚至说只有“吃多菜”这一条腿。那么在这种情况下，我们在教学这个层面，如何做到家校配合，就变得非常实际了。简单说，学校提供的“吃多菜”，那么必然每个家庭提供的就是“一菜多吃”。这是目前比较可行的。

此外，对于一些校外培训机构来说，如果有这个能力，它可以一肩挑，兼顾“一菜多吃”与“吃多菜”，在这样的情况下，它必然会有很高的收费标准。从商业角度来看，这是教育产业高利润的所在。

所以这些问题并不简单。我们天天讲家校配合，到底讲的是什么配合，是不是很多时候流于形式，失于空洞呢？我以为，教育工作者需要思考这些问题，拿出一些方案来做尝试。我的看法是，对于学校的老师来说，至少可以实现，在练习题这个层面上的“一菜多吃”。这是完全可以操作的，老师是有这个能力的。如果我们老师能去做，不光是自己减少了投入（回报却更高），并且是真正的减轻了学生的负担。这就好比我们小学就接触到的统筹问题，烧水、洗壶、沏茶，怎么安排呢？

老师、家长、学生天天叫累叫苦，为什么不去从一些最基本的事情入手呢？学习从来就不轻松，但不是说，学习就没有方法，就不能追求效率。一味的强调吃苦，而毫不关心效率，这难道不是一种失职吗？这难道不是一种推卸责任吗？

我们现在所生活的这个时代，通讯异常发达，人类社会似乎在变小，我们在家里就可以知天下事。但是，我们目前所发生的一些沟通，相当一部分是在做“无用功”。我们并没有充分的挖掘沟通的价值。学科 与学科之间的沟通，可能比较难，习题与习题之间的沟通，难道是难到够不着吗？

好吧，我最后又回到了物理问题：无用功。

==================================

下面讲一个数学问题：负数。

负数是中学数学里的一个难点，就跟小学数学中的分数是难点一样。

当我说“一样”时，到底指的是二者都难，还是指的是二者之所以难是因为难在同一个地方呢？我指的是后者。

分数之所以难，是因为它有双重身份。中间这个分号，既可以当成第三方，当成第三方的时候它就是一个除式的竖写，也可以当成“整体中的一个组件”，这个时候它就是一个数。

负数难在哪呢？负数也难在零有双重身份，一个身份是数值，一个身份是位置。

而在接触负数之前，学生对于0的理解，是数值。0，就相当于没有。但是，在更早的时候，0的身份就是双重的。一方面，它表示数值为0，另一方面，它表示出位置，这样，合起来就是10中的0，是指个位上的数值为0。也就是说，从一开始，0就是双重身份，但是由于我们的教学中并没有专门去讲十进位制的这种安排，所以学生是不大清楚这个问题的，不过这不是主因。

进入负数这个阶段之后，负数的位置跟十进位制中的位置是不一样的。引入了负数之后，0就具备了双重身份，具体带来什么变化呢？

具体的变化，就是何时用加法，何时用减法，“倒置”了。

在没有负数之前，数的方向是没有统一的。比如挣钱，我们就定义成一个方向，借钱我们就定义成了另一个相反的方向。这样，“小王上个月挣了100元，这个月借 了150元，小王的总资产发生了什么变化呢？”我们说，小王整体欠别人50元。这个时候有负数吗？没有。我们是怎么得出了欠别人50元这个结论呢？我们用的减法。

但是引入了负数之后，我们用的是加法。

这样我们就发现了一个问题：加法到底是什么？减法又到底是什么呢？

为什么有了负数之后就有了加减法的倒置呢？

为什么有了负数我们就产生了要统一的想法呢？

这是因为零有位置。

我们看一个具体的例子，来理解，零的位置，到底影响了什么。

当0在a与b的一侧时，若求a点与b点之间的距离，我们用减法。

当0，在a与b之间，也就是c点时我们求a、b两点之间的距离，我们用加法。

要注意，这两种情况下，a与b的位置没有发生变化，但是数值发生变化了。

好，我们想一下，如果我们不能统一，我们在回答这个问题时，是不是就需要知道0在哪呢？0在一侧，用减法，0在中间，用加法。我们必须要知道0在哪。但是我们统一了之后，就不需要知道0在哪了。事实上，a点与b点的位置不变，二点之间的直线距离本来就是不变的。所以我们当然就会想出一种方法来，来解决【要知道0在哪，才知道是做加法还是减法】这个麻烦。

从语言表达的角度来看，正负数方向上的统一，就是数学语言要将自然语言剔出去，这提供了一种书写、运算上的便利。

但是我们总要想一下，当我们“得到了什么”时，是不是还会同时“失去一些东西”？

那么我们得到了这种便利，失去的是什么呢？是直观的感受，是要打破负数之前建立起来的加、减观。

那么我们还要考虑一下，是得多还是失多？

经过思考，我们发现，得多和失多，是一个相对概念。

当用人肉来进行运算时，我们认为得到的多。而用计算机来运算时，我们发现失去的更多！

这是因为计算机把人肉运算这一部分给承担起来了。我们的观念之所以会发生变化，就是因为什么人、用什么方法做事，发生了变化。好比我们现在有语音输入，我们就开始“嫌弃”传统的书写方法了。语音输入本质是把一步变成了两步，人告诉机器，叫输入，机器识别变成文字，叫输出，而传统书写是用人手配合一步输出。

我以为，在负数这个环节里，我们是需要引导学生来认识这些问题的。

我们并不能简单的说“负数好，负数呱呱叫”。这是因为如果我们是这样一种看法，那么我们当然就会认为“学生的脑子不好使，很笨。”而没有注意到，负数的出现，方向的统一与对立，形成了加减法的倒置，其实是一种很大的困难。我们的学生，很难快速学会两条腿走路，更不容易做到自如的在这两种环境 中进行转换、切换。要不然，为什么许多老师自己也不知道负数难在哪呢？

我们还要注意到一个问题，哪怕是不考虑计算机参与，这就是，有了数轴和直角坐标系之后，我们往往更多的是去求距离。正因为这样的使用环境 ，所以我们“认为”统一方向就是最好的。也就是说，从几何发展出来的数学，研究了很多的空间问题。这样，我们的加法就让出了它的地盘，它变得很少使用了。我们后来有很长一段时间，似乎是不用加法这种思维的，我们只是在运算罢了。

这就是为什么很多学生搞不清，为什么a与b的中点是(a+b)/2的原因，他们往往写成了（a-b)/2。这再一次的揭示了，“数值跟位置的不同，学生是没有理解到的。”

学生为什么会认为a点与b点的中点是（a-b)/2呢？他们是从数值角度来考虑的。两点之间的距离不就是a-b吗？那么中点不就是（a-b)/2吗？

而实际上，我们求的是中点的相对位置。什么叫相对位置呢？就是既有位置，又有距离。那么怎么来理解a点跟b点的中点位置是(a+b)/2呢？取平均值。取平均值用的是加法。也就是说，需要做一个转换，把a和b的中点位置，理解成求oa和ob的平均值。这样一次就得到了结果。

那么学生脑中的减法是不是就不行了呢？当然是可行的，学生的问题在于只完成了一步，只求出了距离数值，并且没有注意到这距离指的是谁到谁。我们在距离这个概念上，教得很不严谨，学生往往会把数值跟距离搞混。实际上，数值只是距离的一部分，距离还要指出，是谁到谁。

不难发现，负数难，就难在概念上面。

学生对于由此产生的很多新概念（实际上是旧概念的一些变型）没有吃透。A概念往往与B概念混为一谈，纠缠不清。但我还是那句话，要完成学习，这个成本是必须要付出的，这需要投入时间和精力，不可能一蹴而就。而我们的教学恰好相反，如同在学习分数一样，总想着学生一口吃成个大胖子。同理，在进入代数时，也没有注意到代数中同样有双重身份，一个是符号，一个是数值指代。

我们完全可以得出一个经验：但凡涉及到双重身份的概念、知识，都有很大的学习难度。

================================

这个问题我需要再多说一次。

分数，我们长期给学生提供的是占比模型。这样学生脑中的整体1，就是一种固定的整体1，而不是那种老师希望学生建立的，自定义整体1。

我发现了这个问题之后，我切入的角度就是：整体与局部的关系。

天然1，与自定义1，由谁来决定？由人来决定。从教学效果来看，先从“比”这个概念入手，对于学生建立“自定义1”有很大的帮助。

来看一个简单的例子。

3个苹果跟5个梨，数量比是多少？3：5

3个苹果放在白盘子里，5个苹果放黑盘子里，数量比是多少？3：5

第二种情况中，白盘子跟所有苹果的数量比是多少？3：8

通过这样的对比，让学生体会到，自定义1是由“我”来决定的，同时也注意到，天然1的客观存在（意识存在）。

天然1是一条腿，自定义是1是另一条腿，反复在这两条腿中切换，学生才能学会自如应用。

我可以不客气的讲，中国的分数教学，只强调一条腿，但是要求学生会两条腿走路，这是强人所难——“比”这个概念，在很后面才出现。

至于说到分数中的数与式这两条腿，就更是拎不清了。

我们根本就没有深入的去剖析，约分（比例缩放）跟除式中的商不变在运算上是可以统一的。

如果不知道这一点，学生是不能接受速度是怎么可以用1米/秒来表达的（你好像不存在这个问题，那是因为你从来就没有想过），他们不知道，这是为了运算的便利。这样，许多学生到了中学之后，仍然没有发现把除式竖写的好处。他们不知道这样来书写，很容易节省一些运算，不用先乘了再除，做一些多余功。他们不理解这样书写，更容易观察出哪些可以约分。

我们的教学里，是讲了商不变的。但究竟是怎么讲的呢？

没有充分的讨论，被除数、除数、商，这三个值其中有两个是输入、一个是输出。当输出不变时，意味着什么？输入变，又意味着什么呢？

有没有讨论，其实输入和输出是可以对调的呢？

这些最基本的概念、最基础的认知，根本就没有讲。

=============================

其实这些概念、认知，并非只在数学中得到应用，像这样的“公共地带”，在教学里成了“三不管”，哪门学科 的老师都不讲，都认为“应该”由别的学科 老师来讲。

在现实 生活中，“三不管”地带就是最乱的地带，这又不再次回到了我讲的一个很基础的认知——结合部往往就是难点吗？我们中国的极贫困地区，不就是出现中西部的交接处吗？

我们的老师很多时候跟某些人一样，结合部不管，任它自生自灭，出了乱子才出来所谓的解决一下。另一些老师花了非常多的心思去研究教学，却不知道难点易发区大概会出现在什么地方。缺失方法论的基本指导，常常是费了劲却得不到收获，这是一个需要去思考的问题。

那么我就想问，提高教学质量，从何谈起？！

自然学科 的老师不带着人文知识来授课，人文学科 的老师忽视自然学科，这不恰好就是我们学生分裂的根本吗？！

自然不带着人文，人文不带着自然，理论不带着实践，实践不带着理论，“公共区域”完全没人管，这还教个啥？学个鬼？！

同理，为什么我们的函数教学也是不成功的呢？

这是因为学生长期把关系式理解成了输入输出式（运算式），当他们一看到y=3x时，就懵了，“这是两个未知数，不可能求出结果的啊。”

学生根本就不知道，输入输出式是包含在关系式里面的。就像学生不知道，整体1这个概念，包含在自定义1里面的。

输入输出式，形象的来描述就是因果关系。而关系式呢？是一种天平感。

一个是有方向的，一个是无方向的。一个相当于矢量，一个相当 于标量。

学生为什么在函数之前，很难理解关系式变形呢？就是这个原因。

但如果我们讨论了这个问题，就会知道，矢量是在标量的基础上，增加了方向这个要素。标量是基本型，矢量是综合型。那我们学习当然就要从基本型发展到综合型，又从综合型反向推回基本型。给出一个函数式，再给一个自变量，可以求出因变量，是因为此时变成了综合的【输入输出式】。而关系式变形这种技巧，应用到函数变形，又产生了坐标系位移这一经验，还是从基本型发展成了综合型。

这些个环节，根本就没有引导学生去打通！他们脑中当然就是一块一块碎片。

所有的问题，都当成了基本型来处理，效率自然是十分低下的。

我们怎么让学生明白函数与函数图像的关系呢？完全可以说，前者是个标量，后者是矢量。好比说，我先规定了“天平两边要一样重”。然后我问：当我在天平的左边放一个重50g的果子之后，那么我应该在右边放多重的砝码才能让天平平衡？从标量到矢量就是这样来实现的。先有规定，然后要“去做”，“做出来的结果要合乎规定”。它是这样来建立认知的。

所以我认为，老师要掌握这种方法论：

你A也教了，B也教了，学生就不会解决问题，那说明 你中间有座“桥”，没有架！你要引导自己和学习去把这“桥” 找出来。

比如我讲，从基本型发展到综合型，人们的意识中往往是一种“在原有基础进行增补”，并没有发现，它实际上可以理解成从甲岸到乙岸去。综合型比基本型多出的那个部分，扮演着“桥” 的角色。

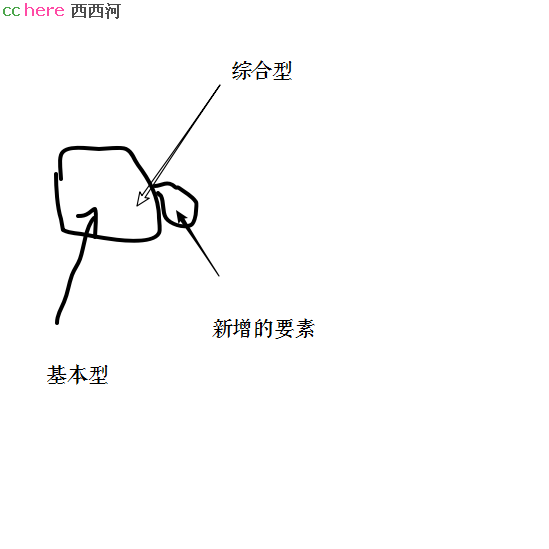
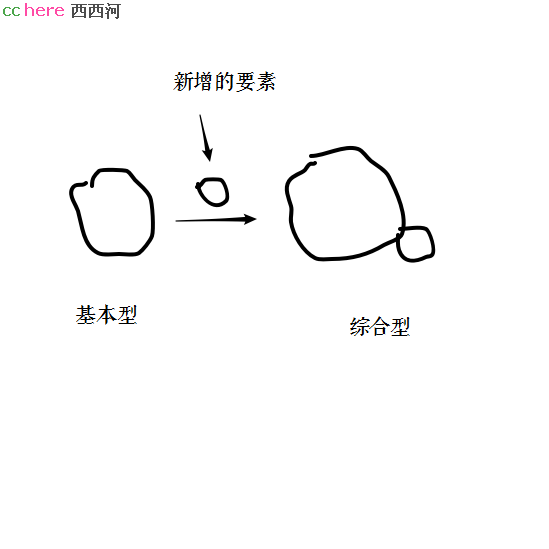
这其实就是整体1与自定义1，占比与“比”！占比不好理解时，我就将它改造成“比”。反过来也一样。我们在结构上做一些变化，目的就是为了找到最优的路径。

==================================

我为什么总讲，其实老师就是搞政治的呢？

搞政治怎么搞？朋友搞得多多的，敌人搞得少少的。老师不把知识、方法、思想团结起来，就是在搞分裂。

在这种情况下，用自定义1，在那种情况下用天然1，那是因为你的能力有限嘛，你仍然在争取团结嘛。

但是我们现在教学呢？是老师带头搞分裂。

到处树敌，最后搞成了“与天下人为敌”，“MD，你们最好全死了，就剩我一个。”这就是不会搞政治的老师教出来的分裂学生。

行为塑造思维。

你的教学长期是分裂式教学，你的学生长期处于分裂当中，你的学生成人之后，就必然是走向分裂的。你的学生一到社会就到处跟人撕逼，跟全世界所有人斗。

我们的社会大分工，本来是要追求一种合力带来的效率上升。

10个工人，每人都有10种需求，一种方法是自顾自的，人人都学会10种技能，每样生产一件。分工之后，是每个人只有一个技能，他一次生产10件，然后跟别人交换。这其实是在减轻人的压力。你是学10样学得快呢，你还是学一个学得好呢？

但是我们今天这个社会变成了什么鬼样子呢？

张三生产了10双袜子，李四生产了10顶帽子。

张三说，因为只有老子会生产袜子，所以你李四必须向我臣服，要不然老子就不卖给你。

李四回了相同的话。

于是两人就开撕。撕的结果是，张三把袜子当帽子戴，李四把帽子当袜子穿。并且两人一见面就是分外眼红，恨不得吃对方的肉，吸对方的血。

这是蠢到家了，宇宙第一蠢。

我就想不通，这些人看书的时候为什么不把嘴巴和耳朵取下来？吃饭的时候为什么不把头发给拔光？本来是抱团取暖，现在好了，变成了抱着一块去死。臣妾不愿意啊！

牢骚发完了，我还要讲一下为什么会这样？

很简单，能力不够大。能力不足以把全世界团结成一个整体。

这个时候我们就会去寻求天然1，所以这个阶段，所谓的民族主义、国家主义就开始抬头了。我们现阶段必然要以退为进。这个阶段是跨越不过去的。

那么这个能力不足到底指的是什么呢？

一个是很容易了解的：信息。

现在信息多，反而造成了【盲人摸象】的恶化。

我张三是生产袜子的，但是我根本就不知道李四是很需要的，并且不知道李四的帽子也是我需要的。所以我生产袜子时，心里是没谱的，李四做帽子也一样。

第二个也很容易理解：就是到底追求的是什么？

是全人类的共同利益，还是我强你弱，我吃肉你喝汤？

这个东西，以前我们经常讲，感觉是虚无缥缈的，但是现在很现实，很骨感，来真的了。假的扯不过去了。

第三个就是三观。

这个东西就跟教学直接挂上钩了。破碎的三观，是学来的，而不是天然的。

那你这个老师没有责任？你推得掉吗？

你今天推掉了，明天学生就要来杀你的头。过去的地主不就是这样吗？不关我的事，最后就被农民剁掉了脑袋。

所以我不客气的讲，老师这个群体，有推卸责任的故意。还不肯回头，必然饱受其害。