- 发帖可能变空内容,邪门暂不知所以然
- 『稷下学宫』新认证方式,24年网站打算和努力目标
主题:数学闲话(闲话开始前的闲话) -- 明日枯荷包
不满足交换律,运算规则当然就不同,不过跟参与的元素的关系不大。正如我所说的,代数结构关心的是结构,也就是元素之间的关系,元素具体是什么其实不要紧,两个其中元素不同的集合,上面都有运算产生关系,只要关系形成的结构一样,那么从代数学的角度来看,其实这两个集合上的代数结构就是同构的,就可以看作是一样的。好像数学家觉得一块石头加一块石头是1+1,一颗钻石加一颗钻石也是1+1,从数学角度来看这两件事作的运算一样;而对其他一些人,这两件事情可能就大不相同喽。
满足交换律的群或者环,当然性质比较好,象乘法满足交换律的环(文中我忽略没有说的是,环的加法被规定为一定要是满足交换律的)以及和它相关的课题,专门有一个数学分支研究它,叫“交换代数”,与之相应的,也有“非交换代数”,这也可以算“两种数学门类”吧。
对于任意自然数n,在自然数集合中比它小的元素有n-1个,假设有个一一对应的映射f能使得两个集合同构,那么在第二个集合中比f(n)小的元素也应该有且只有n-1个,但实际上如果f(n)=x是个偶数,那么该集合中有无穷个元素都比它小。说明这样的同构映射是不存在的。
不知道对不对?而且如果不是对于自然数,而是整数集合,我就不知道怎么证了。
整数集合也一样的。随便取个偶数a和一个奇数b,那么因为是一一对应所以一定有x和y使得f(x)=a,f(y)=b,按照普通的大小顺序x和y之间最多只有有限个元素,但按照“偶数总在奇数后”的顺序a和b之间却有无限个元素。所以这不可能是同构。
没关系,数学面前,男女同构。
以前为了考试,突击复习过这些玩意。
期待其他系列,比如数理统计之类的。:-)
hehe,邪恶的跑掉...
这个只有一节,拓扑我也学得不好,没啥好讲的。(9月2日注:又加了一节“流形”)
前面我们在代数结构(1) 什么是结构以及后面几节里讲了数学结构,还看到了诸如序结构,代数结构的例子,今天讲讲另一种数学结构:拓扑空间。
所谓的拓扑空间,就是具有“拓扑结构”的集合(“集合”和“空间”在这里差不多可以互换,叫“空间”暗示着我们的研究对象是一些图形,形成图形的那些点组成了集合)。我们知道结构是由关系形成的,拓扑结构注重的是于空间中的点之间如何“连”在一起的关系。空间中的各个点的关系通过一些叫“开集”的子集合来表述出来。中学里我们学过实数轴上有“开区间”,那就是一个开集,通过这些开区间就可以在实数轴上定义出一个拓扑空间来。应该说,拓扑结构中的通过开集定义出来的关系,和序结构以及代数结构中的关系比起来,是相当晦涩不直观的。但是它的定义却并不因此而变得复杂,也只有少少的三条公理。
我上面想说的,无非就是拓扑空间也是一种数学结构。把数学研究的对象看作是数学结构的观点,叫“结构主义”。其他学科中比如语言学中也有结构主义的观点,其中有受数学结构主义的影响的部分,但是这些数学以外的结构主义我不熟悉也不关心,就不说了。结构主义的观点是法国的布尔巴基学派提出来的,他们的巨著《数学原理》用结构主义的思想总结和整理了到那时为止的大部分的数学内容。结构主义的观点是相当有效的,甚至可以说是极其有效的,但是有效性在某些数学领域就不是那么明显,尤其是在离散数学方面。我的看法是,在科学研究方面,采取“某某主义”的态度应该是机会主义的:什么主义有用,用起来有效,就用什么主义。这个形而上的问题就扯到这里。
既然是数学结构,当然也讲同构。拓扑空间之间的同构叫做“同胚”,也许翻译者的意思是“一个胚子里做出来的”,但是千万不要字面上这么理解了。粗略地直观地说,两个空间图形是同胚的,如果其中一个可以连续地变换到另一个上去,这里的连续是说“不撕裂,不粘贴”。比如在橡皮膜上画一个圆,我们可以把橡皮膜尽力往四边一拉,这个圆就会被扯大;如果有些地方拉得重,有些地方拉得轻,圆会变形;如果拉得方式巧妙,这圆甚至可以被拉出棱角来,可以变成一个长方形或者一个三角形。但是你不能把橡皮膜给撕裂,把圆周扯裂了,变成了一条不封闭的线;也不能拿点浆糊把圆周上某两个点粘成同一个点,让圆周变成8字形。拓扑学可以看作是研究空间图形在连续的变换下还能保持不变的性质的学科。
从拓扑学家的角度来看,两个同胚的拓扑空间是一样的,是同一个东西,道理跟代数学家觉得两个同构的群或域是同一个东西一样。对于拓扑学家来说,三角形或者长方形或者圆周都是同胚的,是同一个东西,但是和一条不封闭的线或者8字形却不同。所以拓扑学被称为“橡皮膜上的几何学”。圆周是一条一维的曲线,但是更高维的空间也是同一个道理,比如正方体的表面可以想象成是橡皮膜,如果我们往里吹气的话,它会鼓起来变成一个球面,于是从拓扑学家的观点来看,正方体的表面和球面是同胚的,是同一种东西。但是轮胎面你怎么吹气也吹不出球面来,它当中总有一个洞。相反地,如果是一个带一个环柄的茶杯的表面(想象茶杯的表面也是橡皮膜而中间是空的),那么往这个茶杯面里面充气,最后也会鼓成一个轮胎面:茶杯凹下去盛水的部分在充足够气后总会鼓起来,细细的柄也可以鼓得很粗,但是杯柄和杯壁形成的那个孔洞却永远不会因为充气而消失,所以最后会被吹成轮胎面或者甜甜圈的表面。
从另一个方面也可以看出球面和甜甜圈面的不同:在球面上画一条封闭的,不自相交的曲线,然后拿剪刀把球面沿着这条曲线剪开,我们必定会把球面剪成两块。但是甜甜圈面上我却可以画一条曲线,比如这个图上

无论选哪条圆圈来剪开,都不会把甜甜圈面剪成两块。
于是从拓扑学家的观点来看,球面和甜甜圈面是不同的,但是茶杯表面和甜甜圈表面是同胚的。这就是为什么有笑话说:拓扑学家就是那些分不清茶杯和甜甜圈的人。这还不是最恶毒的,我听过的一个版本是拓扑学家搞不清地上有个洞和屁股的区别……
在这里我们可以看见拓扑和几何的关系。拓扑和几何一样也研究空间图形,但是它不关心“两点间的距离”这类性质,因为把橡皮膜扯一扯,两点的距离就变化了。比如几何学家觉得甜甜圈面和茶杯面还是不一样,甜甜圈的那个环是均匀粗细的,茶杯面的柄却比其他部分细。但是拓扑学觉得这没区别。拓扑学关心的是“连在一起”,“怎么连”的问题。球面上的点之间连在一起比较简单,绕无论哪条封闭曲线剪上一圈就可以把球面剪成两块,但是甜甜圈面上的点却似乎“通过好几个方向”连在一起,一圈可能剪不断。这其实是单连通和多连通的区别。又比如橡皮膜上有一个圆,你再怎么扯,这个圆还是把圆里圆外分成了两部分。圆里面的一点和圆外面的一点,你不可能用一条线把它们连起来却不和圆周相交,无论怎么扯橡皮膜(当然还是老规矩,不能扯破或粘贴,也就是变换要连续),圆被扯成奇形怪状,圆里圆外的两点还是被圆周分开。
一讲拓扑学的历史,往往会把欧拉的哥尼斯堡七桥问题拿出来当它的开创问题之一。我总觉得这个问题的解决和图论比较有关系,和今天的拓扑学关系不大,虽然它的解决也用到了类似拓扑学的思想,比如桥的长度和问题无关。见仁见智吧。
如果大家刚开始学拓扑学,那种拓扑学叫“一般拓扑学”又叫“点集拓扑学”,考虑的拓扑空间非常一般,所以会碰上好多怪异的拓扑空间,什么T0啦T1啦T2啦这些空间,T0空间又叫柯尔莫哥洛夫空间,T2空间又叫豪斯道夫空间,后面还有T3,T4,T5等等,甚至还有T2又1/2空间之类的。
其他数学分支的工具可以用来研究拓扑学。我们可以给拓扑空间加上“微分结构”,这是另一种数学结构,这种结构允许我们在拓扑空间上面做类似微积分的计算,这就是微分拓扑。
而用代数学工具来研究拓扑学的分支叫代数拓扑。
我说过分类问题总是学科中的最重要问题之一。在拓扑学里,这个“之一”大概可以去掉。拓扑学家最关心的,就是“一共有多少种曲线”“一共有多少种曲面”之类的问题,当然茶杯表面和甜甜圈表面只能算同一种曲面,而球面则是另一种。
对于某一大类曲面(按行话说是“无边的,紧的,有向的2维曲面”,具体不解释意义了,其中包含球面和轮胎面),要知道其中两个曲面是不是同一种,我们只要数数它上面有多少个洞就可以了,比如球面没有洞,轮胎面有一个洞,而眼镜架的表面则有两个洞……洞的个数一样,那么它们就同胚,个数不一样,它们就不同胚。于是茶杯面有一个洞,它就和轮胎面同胚。洞的个数行话叫“亏格”,不要问我为什么取这名字,我也不知道。我们看到亏格就是刻画这一大类曲面的工具。不仅如此,亏格完美地在刻画了这个大类的曲面:本来想知道两个曲面是否同胚,我们得按照同胚的定义,找到一个一一对应,证明这个一一对应还保持拓扑结构等,麻烦得要死,现在好了,数数有几个洞,两个曲面同胚当且仅当亏格相等。而亏格是一个整数,在这里,我们看到了一个用整数来刻画某一大类曲面的方法。
在更高维的拓扑空间上,光用数来刻画空间性质就比较不方便了,而代数拓扑就可以用群这样的代数结构为工具,来代替数来刻画拓扑空间的性质,比如上面所说的单连通和多连通的性质,就可以用群来表达出来。我会在有关代数结构的帖子里更具体地讲述一些这方面的内容。
本帖一共被 2 帖 引用 (帖内工具实现)
恭喜:你意外获得【通宝】一枚
鲜花已成功送出,消耗 铢钱 1 个,可能得宝。可通过工具取消
提示:此次送花为【有效送花赞扬,加乐善、声望、帖得花总
只有偶尔在cchere里看看,还经常出现网页无法打开的情况。
好象老铁出新政了?对我等潜水党打击实在太大了。
刚才在楼主帖里测试过,第一页楼主7个帖子吧?花出3宝,我2您1。呵呵。
我还是把帖子保存下来看吧。天晓得明天还能不能上来。。。哎
鲜花已成功送出,消耗 铢钱 1 个,可能得宝。可通过工具取消
提示:此次送花为【有效送花赞扬,加乐善、声望、帖得花总数】。
请认领~
前世不修都能这样,如果修了,那.... ![]() 哈哈,开玩笑的啊
哈哈,开玩笑的啊
再添一节拓扑方面的东西:流形。
流形是一种特别的拓扑空间,它的每一个足够小的局部,看起来都象是一个欧几里德空间的一个局部。欧几里德空间就是我们平时熟悉的直线,平面或者三维空间,或者更高维的平直空间。欧几里德空间的性质是再好没有了。
如今除了地平协会的顽固分子们,大家都知道大地是个球,我们站着的这个地面,如果忽略其上面(从地球大小的尺度来说)不起眼的坑坑洼洼,是一个球面。拿张中国出版的世界地图来看,会把中国放在正中,非洲和南美处于最左和最右端,但其实它们只不过隔了一条狭长的太平洋,格陵兰岛则一大块处于右上角,一小半处于左上角,其实这两块是紧连的一个大岛。如果是欧洲出版的世界地图,那就又是另外的样子,格陵兰岛成一整块了,但轮到其实处于狭窄的白令海峡两侧的西伯利亚和阿拉斯加分处地图的左右上角。你不可能在一张平面的纸上很好地显示地球上所有地区之间的相邻关系,总有一些其实靠在一起的地方,在平面地图上被画成离得很远。要正确地展示地球上所有地区之间的相邻关系,同样是球面的地球仪是一个好得多的选择。
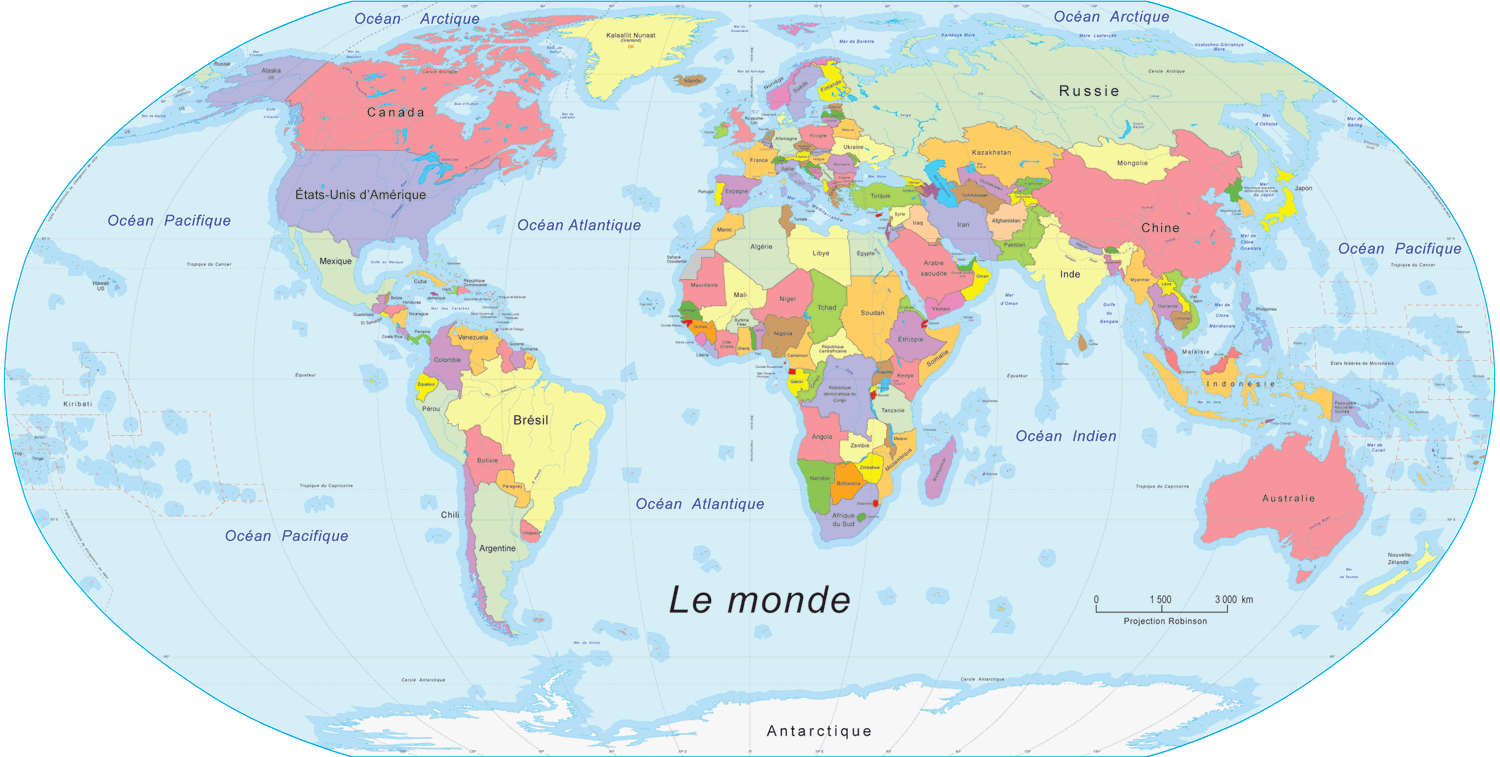
但是这不等于说无论什么地图都得在球面上画。为了画出某个城市的地图,画在平面的纸上足矣,它上面的各个区域之间的相邻关系都是实际的相邻关系。地球上任何一个面积相对较小的区域的地图,都可以画在一张平面的纸上,一张纸可以看作是一个平面的一个局部。
这样我们可以看出,虽然从整体上来看,球面和平面是大不一样的,但是从局部来看,球面的局部和平面的局部却差不多。轮胎面也一样,从整体来看,轮胎面和球面以及平面都很不一样,但是从局部来看,轮胎面的局部和平面的局部也差不多。所以球面和轮胎面都是流形的例子。轮胎面和球面的局部都和平面也就是2维欧氏空间的局部差不多,所以它们都是2维流形。平面本身当然也是2维流形。2维流形的一个通俗名字当然就是曲面。
1维流形(通俗名字拿手指头也想得出来,是曲线)的例子是圆周。圆周的每个局部看上去都象是直线的一部分,但是整体看起来却和直线是不一样的。直线也是1维流形。其实1维的(连通的)流形就只有这两种:圆周和直线。两个不相交的圆周算不算1维流形?也算,但是因为两个圆周不连在一起,可以由连通的流形简单地组合出来,我们对它们不是很感兴趣。
8字形,或者说一条自己和自己相交了的曲线是不是流形?不是。虽然8字形的大部分的局部都和直线差不多,但是如果我们看看那个交点和它周围的情况,我们会发现那个地方和一条直线的局部不一样,到是和两条直线相交的交点处的局部差不多。所以这就不是流形了,那个交点被称为一个奇点。
高于2维的流形当然也存在,局部和3维欧几里德空间差不多的是3维流形,局部和4维欧几里德空间差不多的是4维流形,……,这些流形就比较难以直观想象了,但是照样还是可以定义和研究。最简单的高维流形,一种就是高维的欧几里德空间本身,一种是高维球面。参考(2维的)球面在三维欧几里德空间中的定义方法,我们可以定义3维的球面:4维的(实)欧几里德空间中的每点由四个实数组成的坐标来表示:(w,x,y,z),如果我们考虑这个四维空间中所有满足w^2+x^2+y^2+z^2=1的那些点,这些点就形成了3维球面。类似地可以定义更高维的球面。
象球面以及轮胎面这样的流形,和象平面这样的流形比起来有一个特点,它们不像平面那样一摊开来就无边无际的,它们看上去处在一个有限的范围里。球面以及轮胎面这样的流形,还有一个特点就是它们没有边界(平面也没有边界,但是半平面就有边界,莫比乌斯带也有边界)。这样的处在一个有限范围内,又没有边界的流形,是具有非常好性质的流形,数学家们叫它们是“紧的,无边的”流形。“紧”又叫“紧致”,是指某种意义上的有限。拓扑学里一说“紧”,总是和有限有关系,也有很多种似“紧”不“紧”的概念,比如预紧,仿紧或伪紧,列紧,可数紧等等,学起来有点让人头痛。不过就是一条,“紧”总意味着某种有限。“紧的,无边的”合起来,又叫“封闭的”。
对在有限范围内,又没有边界的这些行话叫“封闭的”流形,数学家们研究得比较多。前面在数学闲话(二)——拓扑(1)拓扑空间这节中就提到过,数学家们对于2维的这类流形的分类已经了如指掌了,就是用“亏格”来分。不过这里说得不是很严格,因为如果对照上一节我说的关于按亏格分类的叙述,那里还有另一个条件是“有向”的。这个条件也很有意思,所谓有向,就是作为曲面,有两个方向,比如球面有里面外面之分,轮胎面也有里面外面之分。在轮胎外面爬的蚂蚁,不把轮胎咬出个洞来,是爬不到里面去的。但是同样也有无向的曲面,最著名的就是莫比乌斯带了,只有一个面。我想现在在读这篇东西的朋友大概都知道什么是莫比乌斯带,所以就不详细说了。


但是莫比乌斯带是有边的,不过也许大家还知道克莱因瓶,这就是一个“封闭的”却“无向”的2维流形的例子。

不管是有向的还是无向的,2维封闭流形(曲面)的分类数学家都搞得很清楚。有向的用亏格,至于无向的就复杂点,但是也没问题。但是高维的封闭流形的分类,就困难得一塌糊涂(在某种意义下我们甚至可以说,这个问题是不可解决的)。关于高维的流形的分类,我会在讲代数结构的“庞加莱猜想中的群”一节中再多讲一些。
本帖一共被 1 帖 引用 (帖内工具实现)
喜欢这样的文章,深入浅出,还能明白很多概念,比如这里的流型。
有个问题:莫比乌斯带是可以很容易制造出来,一条纸条扭一扭两端一粘就是了;克莱因瓶能实际制造出来吗?看图没什么,可实际想想制造工艺,又觉得不好说。不知道有没有哪位知道?