- 发帖可能变空内容,邪门暂不知所以然
- 『稷下学宫』新认证方式,24年网站打算和努力目标
主题:【翻译】概率随机及编程 (一) -- 东方射日
十月底被公司裁员,还算幸运吧,十一月中就拿到一个offer,谁说是contract的,但毕竟是有工作了,而且公司还是一个巨型的软件公司,应该对以后找工作有帮助吧。不过俗话说“骑驴找马”,这不,就继续找看看有没有permanent的职位,同时多找一些算法题做做,题海题海,说实在,还是题海最管用。
这不,找到一个好网站:Topcoder.com,上面有大量的算法的编程题,同时还有一些很不错的文章,推荐给大家看看。同时想自不量力,翻译一些文章给不喜欢(本人就是一个)看英文的人参考参考。对你有帮助呢,那就算我为大家在经济危机中多一条生路做一点自己的微薄贡献(当然鲜花是一定欢迎的)。如果有错误或不妥呢,也请高手不吝赐教,鲜花是一定会有的。
原文的链接在外链出处。看了一下,好像没有提到这些文章的版权问题,就先自作主张认为没有关系吧,如果大家发现有版权问题就请尽快来消息告知。
不过里面的很多例题都是有版权的,我们只能大致描述一下,具体的内容还是请大家注册一个帐号到上面去看吧。相信我,如果你是软件工程师,而且对算法感兴趣,这一定是值得的。
翻译中才发现翻译的困难,有的明明看起来很好理解的,用中文表达的话,还真就有点绕口。雅是不敢求的,不过翻完后,自己又都读了一篇,应该理解是不会有太大的困难吧,只希望“信”上不要有太大的差距。
在上述链接中有很多文章,我不敢保证有时间都翻译出来,有一篇算一篇吧。希望有人也愿意翻译其他一些文章。好吧,就随机地从这篇文章开始吧:
http://www.topcoder.com/tc?module=Static&d1=tutorials&d2=probabilities
概率随机及编程
作者:supernova
前言
有种说法,生活是概率的学校。概率论让我们的每一天都生活在风险评估中。假设有一个考试,总共有20门可能要考科目,而你只有时间准备其中15门。那么考了两门你都准备过了的科目的可能性是多少?这是我们生活的世界会带给你的一个简单的问题。生活是一个非常复杂的事件链,其中几乎每件事都可以想象成一定的概率。
赌博已经是我们生活的一部分,这其中显而易见牵涉到了概率。虽然赌博的历史可以追溯到史前时代,但是直到17世纪,随着近代数学基础的建立,才开始被研究。这始于一个Chevalier de M(一个经常通过赌博增加财富的贵族)向Blaise Pascal提出的一个简单问题:扔24轮骰子是否可以得到两个6点?
一些编程问题是由现实问题引申来的,通常我们会描述一些状态,并解释一些运行的规则。但你会发现如果这是一个概率相关的问题时,解决的方法就并不那么显而易见。这可能是因为在编程学习、竞赛中,概率经常被忽视而没有作为主要的研究点和考察点。
在采用一些必要的算法解决这类问题前,你必须有一些数学的准备知识。下一章将介绍概率的基本原理。如果你已经在这方面有点经验的话,也许你可以跳到下一章:概率计算。在那以后我们会对随机算法进行简单的讨论,随后列出了一些练习的题目。这最后一章也许是最重要的:练习!关键就是多练习。
基础
解决概率问题很像是在做实验,输出就是一个实验的结果,这包含其他一些不确定的因素。对于一个概率实验所有可能的输出,我们称为采样空间。每种可能的结果在采样空间中占且仅占据一个单位,通常用符号S代表。让我们考察如下实验:
扔骰子一次:
采样空间 S={1,2,3,4,5,6}
抛两个硬币:
采样空间 S=({正,正},{正,反},{反,正},{反,反})
我们定义我们实验一次为一个事件。这样,一个事件就是采样空间S的一个子集。如果我们用E来代表一个事件,那么有E S。如果一个事件仅包含一次采样空间的结果收集,那么我们称为简单事件。对超过一个结果的收集,我们称为复合事件。
事实上我们通常仅对某一特定事件的概率感兴趣,记为P(E)。我们定义P(E)是0到1间的一个实数。0表示这是不可能的事件,而1则表示确定事件。
我们前面说过任何一种结果都是采样空间中的一个单位,那么我们可以有如下公式:
P(E) = |E| / |S|
一种事件发生的概率是该类事件(特定结果发生)的次数除以各种可能事件(各种结果发生)的总次数。要理清事件之间的关系,我们可以应用集合的知识。例如考察扔骰子的实验,我们前面说到这实验的采样空间 S={1,2,3,4,5,6}
现在我们考察如下事件:
事件 A = '点数 > 3' = {4, 5, 6}
事件 B = '点数为奇数' = {1, 3, 5}
事件 C = '点数为7' =
A∪B ='点数大于3或为奇数' = {1, 3, 4, 5, 6}
A∩B ='点数大于3或为奇数' = {5}
A' = '事件A没有发生' = {1, 2, 3}
那么我们有:
P(A∪B) = 5/6
P(A∩B) = 1/6
P(A') = 1 - P(A) = 1 - 1/2 = 1/2
P(C) = 0
解决概率问题的第一步是定出采样空间,然后你就需要确定期望结果的数目。这就是传统的解决办法,但是具体的解决方法是多种多样的。例如在”Quiz Show”(例题都是有版权的,请自己登录网站看)问题中,解决的关键是考虑所有的可能性,这数目并不多。通过简单的分析,我们可以定义一下样本空间
S = { (wager 1 is wrong, wager 2 is wrong, you are wrong),
(wager 1 is wrong, wager 2 is wrong, you are right),
(wager 1 is wrong, wager 2 is right, you are wrong),
(wager 1 is wrong, wager 2 is right, you are right),
(wager 1 is right, wager 2 is wrong, you are wrong),
(wager 1 is right, wager 2 is wrong, you are right),
(wager 1 is right, wager 2 is right, you are wrong),
(wager 1 is right, wager 2 is right, you are right) }
该问题要求你找到你最有可能获胜的下注额,为了计算一定下注额的获胜概率,我们可以分别计算8种情况下各人的最后得分。以下程序可以进行这个计算:
int wager (vector scores, int wager1, int wager2)
{
int best, bet, odds, wage, I, J, K;
best = 0; bet = -1;
for (wage = 0; wage ≤ scores[0]; wage++)
{
odds = 0;
// in 'odds' we keep the number of favorable outcomes
for (I = -1; I ≤ 1; I += 2)
for (J = -1; J ≤ 1; J += 2)
for (K = -1; K ≤ 1; K += 2)
if ( scores[0] + I * wage > scores[1] + J * wager1
&& scores[0] + I * wage > scores[2] + K * wager2) { odds++; }
if (odds > best) { bet = wage ; best = odds; }
// a better wager has been found
}
return bet;
}
另外一个很好的例子是“Pipe Cuts” 。这也可以用类似的方法解决。对这类只有有限可能(且数目不是太大)的情况,我们可以利用这种穷举法计算。
对于一系列独立事件:E1,E2......EN,有两个经常会提到的问题(应该你们也已经遇见过):
一:所有事件发生的概率是多少?
二:至少一事件发生的概率是多少?
要回答第一个问题,我们可以先考虑第一事件E1发生的概率,如果E1不发生,上述一将永远不会满足。那么我们可以确定必须有E1以P(E1)的概率发生了——即有P(E1)的可能性——我们才需要继续检查下一事件(E2)。而E2发生的概率是P(E2),接着我们就可以重复这一步骤。正如我们上面说到概率是用0到1间的实数定义的,那么显然我们可以用以下公式计算所有事件发生的概率:
P(all events) = P(E1) * P(E2) * …... * P(EN)
对于第二个问题,更容易的方法是计算任一事件都不发生的概率。(也就是说有反事件发生的概率)我们可以有:
P(at least one event) = 1 - P(E1') *P(E2`)*......* P(EN')
这两个公式非常重要,请在继续下一章前理解他们。
本帖一共被 2 帖 引用 (帖内工具实现)
生日错觉
这里有一个很好的例子有助于大家理解我们上述讨论的概率。这就是经典的生日错觉问题。这就是说,如果有23个人在一间屋子里,那么其中至少有两个人生日相同的概率将大于50%。这和我们的直觉好像是矛盾的,但是数学上却可以证明这是真的,我们的直觉是错的。“BirthdayOdds”问题要求你计算最少需要多少人才能使两个人的生日相同的概率大于某一值。
首先,我们可以注意到互补的问题可能更容易解答:“N个随机的人生日各不相同的概率是多少”。解决的思路就是从一个空房间开始,逐一添加一个个人,计算生日与里面所有已有人不同的概率。
int minPeople (int minOdds, int days)
{
int nr;
double target, p;
target = 1 - (double) minOdds / 100;
nr = 1;
p = 1;
while (p > target)
{
p = p * ( (double) 1 - (double) nr / days);
nr ++;
}
return nr;
}
这个所谓的生日错觉有很多实际的应用,其中之一就是“Collision”问题。算法和上面基本是一样的,有一个要注意的事项是,有时事件本身可能会改变样本空间。
有时,一些概率问题是比较费解的,例如上面所的生日错觉问题似乎违背了我们的常识。但是利用前面的公式,我们可以计算出正确的结果。不过你如果想成为一个概率专家,还需要更多的对数字的“感觉”。这种感觉一部分是天生的,另一部分可以后天通过学习和练习来培养。做一下外链出处上的测试,你一则可以了解自己对数字的感觉,二则也会对一些基本的概率问题有更多的理解。
概率计算
在本章中,我们将采用一些例题来计算非独立事件的概率,也就是说一件事件的发生将影响随后事件发生的概率。我们可以用图来组织这些事件,节点是时间,边是事件间的依赖关系。在我们计算不同事件的概率时,很类似于我们在图上前进。我们从图的根节点开始,这就是事件开始前的初始状态,并且可以设置根节点的概率为1。然后依据不同的情况,我们考察概率是如何响应分布的。
嵌套的随机数
Nested Randomness 问题。(大致就是计算随机函数嵌套情况下的概率,具体描述请上topcoder参看)
这一问题看起来让人退缩。但是据说有人已经指出,这只是几条线的问题。
第一步,我们很明确我们要做什么,随机函数Random(N)被调用并返回一个在0到N-1间均匀分布的随机整数。这样,也就是说每个整数出现的概率是1/N。如果我们将这一结果作为下一次调用随机函数的输入,我们可以得到所有Random(Random(N))结果的概率。为了好理解,我们以N=4为例:
第一步,各个整数有相同的概率1/4
第二步,以下四个函数各有1/4的可能被调用Random(0);Random(1);Random(2);Random(3).Random(0)返回错误,Random(1)返回0;Random(2)各有1/2的可能返回0或1;Random(3)则各有1/3返回0,1或2
第三步,Random(0)有1/4+1/8+1/12的可能性被调用,Random(1)的可能性则为1/8+1/12;Random(2)的可能性为1/12
类似的,第四步,Random(0)的可能性是1/4而Random(1)的可能性是1/24
第五步,我们只有Random(0)的可能
所有过程在下图中描述:
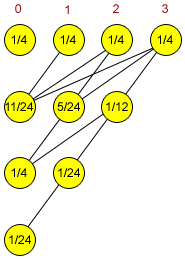
源代码如下:
double probability (int N, int nestings, int target)
{
int I, J, K;
double A[1001], B[2001];
// A[I] represents the probability of number I to appear
for (I = 0; I < N ; I++) A[I] = (double) 1 / N;
for (K = 2; K ≤ nestings; K++)
{
for (I = 0; I < N; I++) B[I] = 0;
// for each I between 0 and N-1 we call the function "random(I)"
// as described in the problem statement
for (I = 0; I < N; I++)
for (J = 0; J < I; J++)
B[J] += (double) A[I] / I;
for (I = 0; I < N; I++) A[I] = B[I];
}
return A[target];
}
如果你在这个问题上有点心得,你可以再试试以下五个问题:
ChessKnight问题:为每个棋盘格分配一个该路,每一次移动计算下一步每格的概率
DiceThrows问题:计算两个玩家扔骰子各种可能的结果
RockShipping 问题:采用同样的思路,确定你定义了正确的湖的模型
PointSystem问题:用可能的(x,y)矩阵来建立时间的采样空间
VolleyBall问题:类似于上一问题
本帖一共被 1 帖 引用 (帖内工具实现)
下面让我们再看看另一个问题,GeneticCrossover该问题是处理条件概率的。这要求你基于它由它父母那继承来的基因来预言一个动物的适应性。注意一下问题的描述,基因有两种可能的情形,一是显性基因,不依赖于其他的基因;二是隐性基因,是否表现出来依赖与其他基因。
在第一种情形,假设P是某一显性基因表现出来的概率,那么P只有四种可能:
至少有一个双亲有一对显性基因(P=1)
双亲都仅有一个显性基因(P=0.5)
仅有一个双亲有有一个显性基因(P=0.25)
双亲均没有该显性基因(P=0)
现在我们在考虑第二种隐形基因的情形。这依赖性让事情变得有点复杂,因为双亲的基因也有可能是隐性基因等等。要判定一个一个隐性基因表现出来的概率,我们要判断该基因在染色体上被携带并传递下来这个事件的概率,为了让隐性基因表现出来,我们需要这个事件在双亲两边都发生。
以下是该问题的源代码,我们采用了递归:
int n, d[200];
double power[200];
// here we determine the characteristic for each gene (in power[I]
// we keep the probability of gene I to be expressed dominantly)
double detchr (string p1a, string p1b, string p2a, string p2b, int nr)
{
double p, p1, p2;
p = p1 = p2 = 1.0;
if (p1a[nr] ≤ 'Z') p1 = p1 - 0.5;
// is a dominant gene
if (p1b[nr] ≤ 'Z') p1 = p1 - 0.5;
if (p2a[nr] ≤ 'Z') p2 = p2 - 0.5;
if (p2b[nr] ≤ 'Z') p2 = p2 - 0.5;
p = 1 - p1 * p2;
if (d[nr] != 1) power[nr] = p * detchr (p1a, p1b, p2a, p2b, d[nr]);
// gene 'nr' is dependent on gene d[nr]
else power[nr] = p;
return power[nr];
}
double cross (string p1a, string p1b, string p2a, string p2b,
vector dom, vector rec, vector dependencies)
{
int I;
double fitness = 0.0;
n = rec.size();
for (I = 0; I < n; i++) d[i] = dependencies[i];
for (I = 0 ;I < n; I++) power[i] = -1.0;
for (I = 0; I < n; i++)
if (power[I] == -1.0) detchr (p1a, p1b, p2a, p2b, i);
// we check if the dominant character of gene I has
// not already been computed
for (I = 0; I ≤ n; I++)
fitness=fitness+(double) power[i]*dom[i]-(double) (1-power[i])*rec[i];
// we compute the expected 'quality' of an animal based on the
// probabilities of each gene to be expressed dominantly
return fitness;
}
随机算法
确定算法对于一个固定的输入总为产生固定的输出和同样的运行时间。随机算法则不同,它每次运算的运算路径,运算结果等都可能是不同的。基本上我们有两种随机算法:
门蒂卡罗算法(Monte Carlo algorithms):可能产生错误的输出,我们只限定失败的概率(参考:外链出处)
拉斯维加斯算法(Las Vegas algorithms):总产生正确的输出,唯一的变量是运行时间,我们研究运行时间的分布(参考:外链出处)
随机算法的主要目的是建立一种更快和更简单的解决方法。另一个好处就是能够处理一些困难的没有确定解决方案的问题。现在这些算法已经是大家感兴趣的研究方向并且已经找到一些针对困难问题的简单方法。(译者注:现在时髦的神经网络算法,遗传算法等在一定程度上就是随机算法的应用。神经网络算法中传递到下一层神经元的信号强弱和遗传算法中的基因突变都应用了随机的原则,感兴趣的朋友可以自己搜索资料)
还有一些问题有很多可能的解,其中一些是可接受的优化解(未必是最优解)(译注:原文中都使用了“optima”一词,但是依据上下文及我的理解,这里应该有优化解和最优解之分,传统的确定算法注重于寻找最优解,但是有些问题我们是无法以确定的时间、空间复杂度找到最优解,这种情况下我们往往转变注意力到寻找优化解,即是可以接受的解决方案,但并不一定是最优的。例如传统的背包问题就是这样一种问题,现在的数学除了穷举,仍旧无法在一个确切的时间、空间复杂度内找到最优解)。传统的方法是以一个确定的规则来一个个进行比较以寻找最优解。但是我们如果不能确定最优解在所有解中的位置,这样确定算法有时甚至无法在确定的时间找到最优解或优化解。随机算法的优势是不确定搜索的次序,这样,当优化解的集合是集中在某一区域的时候,随机算法(寻找优化解)的性能通常会比较好。例如“Queen Interference”(”8皇后问题”)
随机算法在面对恶意攻击是特别有效,在这种情况下对方故意输入错误的数据给算法。这在加密系统中有广泛应用。(译注:对这一段我还不是很理解,原文如下:Randomized algorithms are particularly useful when faced with malicious attackers who deliberately try to feed a bad input to the algorithm. Such algorithms are widely used in cryptography。)
随机算法在编程中也有其应用的意义,例如你有一个有效的算法,但是在一些退化的输入时,该算法会特别特别慢,那么你可以考虑随机算法。一个算法对各种输入都应该能在可以接受的时间内给出解答。否则即使是正确的,该算法也是不可行的。这就是我们在编程时特别强调“最坏情况下的运行效率”。
对程序的评判
如果你是编程竞赛的评委,你有15分钟的时间来检查其他程序员的BUG。这些提供给你的其他人提交的程序,在以下两种情况可能有时会引起你额外的注意:
一、提交的程序象是时间紧急时的仓促之作,对于大部分输入是失败的
二、算法经过比较彻底的测试,错误(或超时)的可能几乎是没有
对于第一种情况,你所要做的事是首先确定编程人员是不是一个成功的有经验的高手,如果是,在你考虑扔掉它前最好仔细研究一下他的算法,确定你了解他的用意。同时你要考虑一下其他因素,包括其他人对他的评价,算法的精确性,完成的时间,修改的次数等。(译注:本文作者是在topcoder,一个编程竞赛网站上贴的该文章,这段的意思是算法思路比实现算法更重要)
“随机”到底怎么用
在很多优化问题中,可行的优化解在所有可能解中的分布是不一定的。简单的方法是用一些不同的例子来观察算法的结果。做这样一个模拟通常相当快,且这试验本身也会给你提供一些解决方法的额外线索。
Max = 1000000; attempt = 0;
while (attempt < Max)
{
answer = solve_random (...);
if (better (answer, optimum))
// we found a better solution
{
optimum = answer;
cout << "Solution " << answer << " found on step " << attempt << "\n";
}
attempt ++;
}
练习:
略(这可是作者说最重要的一部分,俺咋就给略了呢?)
恭喜:你意外获得【通宝】一枚
谢谢:作者意外获得【通宝】一枚
鲜花已经成功送出。
此次送花为【有效送花赞扬,涨乐善、声望】
不过对“神经网络算法,遗传算法等在一定程度上就是随机算法的应用”这个说法有点不同的看法,神经网络实际上是经常用于逼近实数值、离散值或者向量值的目标函数。可能有些神经网络算法某些部分会采用随机算法来优化训练过程和更好地拟合结果(这方面不是很清楚,究竟如何不好妄断),但是就我所知,核心算法跟随机算法并没什么太大的关联的。
其实关于神经网络我也就看过小半本很薄的书(标准的一瓶底儿醋 - -!),随便说说,权当是抛砖引玉,错了勿见笑~
你说的对,神经网络的核心不是随机算法,而应该是那个活化函数(常用的s函数或双曲正切函数)。并且传统的神经网络算法如你所说,没有用到随机算法。
以最简单的三层前馈神经网络为例,输入层在接受输入后,传导给隐藏层,传导的过程则是输出值乘以权重加上一定的偏差值。各神经元间连接的权重和偏差是通过回馈函数进行训练修正的。
这种不带随机的神经网络有一个特点,就是如果不断给出输入同样的输入,经过长时间的回馈训练,其行为会逐渐逼近线性函数,稳定地给出我们希望的输出值。类似于我们说说的条件反射。
放在日常生活中,一个熟练工人我们可以说他出错的可能性很小,但是我们不会说他绝对不会出错。
所以在游戏的人工智能中,我们在神经网络中通常会引入一些随机量,也就是人为引入些噪音。对权重和偏差随机有些变化。这样在对同样输入长期训练后仍旧会有一些出其不意的变化。可能是更好的决策,更多可能是大脑短路的自杀。
其二,隐藏层通常是非线性的活化函数对传递来的信号分析后,输出到输出层,通常会活化超过一个的输出神经元。一种方案是采用赢家通吃的办法,将活化值最大的神经作为该算法的输出。但是更常用的算法是将各个神经元的输出作为权重,采用随机函数来决定该算法的输出。
所以准确的说法,我应当将“神经网络算法是随机算法的应用”修改为“神经网络算法也应用了随机算法”
多元线性回归是否要求假定样本服从正态分布?一元线性回归是否也有这样的要求?
比如,我有一批样本值y,与两组指数x1,x2(二者是独立的指数)都有极显著的正相关(r>0.6),我想建模,到底是与x1、x2分别一元线性回归呢?还是与x1、x2多元线性回归?
无论哪一种回归建模,是否需要样本服从正态分布呢?
谢谢!
真是好贴
作者意外获得【西西河通宝】一枚
推荐成功!
当时找工作的时候多亏它了
读书的时候只为了凑结果,程序写得一塌糊涂。结果要面试了,把那个std lib得tutorial打印下来,飞机上扫了几眼,结果面世的时候大部分相关的编程问题都能应付。
回归模型与数据分布都是用来解释数据的,具体是否用回归模型还是分布取决于哪一个能够更解释数据本身,至于是否服从正态分布,完全不相干,因为还有很多别的分布可以服从或者没有什么分布可以服从。
并没有特定的假设要求数据服从正态分布,倒是很多经济学上的模型喜欢用正态分布做假设,无它,仅仅简化问题而已(正态分布数据易于解释)。
具有相关性的两列数组,分别模型与多元模型都可以,但仍取决于你的目的和模型的效率。唯一区别,一元假设INDEPENDENCY,多元要考虑X1*X2的效果。初步倾向于多元。
送花!
对于系统来说。彼此的要素本身不是相互独立的。
很多时候他们之间会产生互相的影响。如果通过
研究要素的性质来还原系统往往得不到正确的认识。用这样的结果去决断往往会得到和目标不一致
的结果。本身系统就会体现一些自有的特性。我觉得以现在的数学水平去衡量非线性的影响是很困难
的事。而且更为头痛的是只有人观察到某些结果时
才会去思考产生的要素,而这些要素往往是在很长
时间之前就发了作用。这就是很多时候在危机发生
以前人们毫无知觉的缘由。有的时候一个干预的要素会产生一系列的结果。如果单独考量这些结果作为变量输出研究也是无法对系统产生正确认知的。
而影响这些结果的要素可能更被间接的影响所支配。比如国家之间重要的双边关系往往会被其他国家之间的关系所支配影响。要命的是一个主观的
输入会产生一系列和期待输出不相符的结果。但
并不是意味着改变没有意思而是需要有连续的影响。这本对数学方法的引入就提出了挑战。这一点
在生物学研究上也有所体现。大自然的复杂超出了
我们的常识。我们的认知还出于比较低的阶段。
有段时间没上网了,先给你的答复送朵花
统计其实是算法中一个重大分支,也有大量的职位要求熟悉这类算法,例如data mining之类的。
其实我对这个分支几乎是各菜鸟,若水的问题正点到我的弱点,多谢老兄回答,替我藏拙了。