主题：【原创】由一个简单的面试题想起的 -- 东方射日

有一个N层的货架，你需要知道特定包裹在该货架上的最大＇安全高度，即从M（１＜＝M＜＝N）层摔下，包裹不会摔坏。

前段时间换工作，经历几个面试，有一题是这样的：

有一个N层的货架，你需要知道特定包裹在该货架上的最大＇安全高度，即从M（１＜＝M＜＝N）层摔下，包裹不会摔坏。

给你一个试验包裹，如何以最快的方式找到M？

－－－－我当时就是一愣，自演言语说从一层开始一层层往上试。那么还有什么更好的方法吗？面试的人打断我,别想太多，那就是唯一的方法。

他接着问,如果给你两个试验包裹，如何以最快的方式找到M？给出你的解答！

我首先想到的是两层两层地试第一个包裹，不过马上自己否定了，仔细想了下，在白板上写：

第一个包裹取步长为s向上试，直到摔坏为止，试验次数为 ：

t1 = INT[(M-1)/S]+1 (INT指取整)

第二个包裹在第一个包裹确定的区域内一层层向上试，直到摔坏为止，则最后一次没有摔坏的那层就是M。共试验：

t2 = M-MOD[(M-1)/S]*S

当时就想到，从常识上，Ｍ越大，应该选用的Ｓ就应该越大，也是应该存在阀值使ｆ（Ｓ，Ｍ）＝（ｔ１＋ｔ２）＝ｆ（Ｓ＋１，Ｍ），算出Ｓ＝（ｓｑｒｔ（４Ｍ－１）－１）／２，计算中忽略了取整和取摸运算子。

不过我仔细再一想，不对啊，我们事前并不知道Ｍ，只知道Ｎ，如果我们假设每层包裹摔坏的机会相当，最优解就是使总测试平均值最小的步长S值：

{SGM（M=1,N）[t1 + t2 ]} / N (SGM: 求和运算子)

解上式 得S＝f(N)

我只做到这一步，至于求和和算最小值我也不会. 还好，对方说＂Good enough＂

回来后仔细想拉想这题，觉的学问还不只这些，自己又提出以下问题:

前面我们一直是想找出试验第一个包裹使平均试验次数最少的最优解步长S，并且这里我们忽略了我们又有另一个假定在里面，就是假定Ｓ是一个定值能使解最优。但是如果采用变化步长，是否有更优的结果呢?

比如我们采用递增步长，直觉上觉得菲波那契级数或者其他的递增级数可能有更好的结果。但是自己数学能力实在不够，无法证明和计算。

河水深了，什么大鱼都有。就抛个砖等大鱼来吧。

======

又仔细想了，应该采用递减步长，即第一个包裹试验步长为剩下层数的sqrt(N) ＋1/2。

例如N＝１５层时，第一个包裹试验第４、８、１１、１３、１４、１５层，这样平均尝试次数为６７／１５次。如果采用固定步长４，平均尝试次数为６９／１５次

但是还是不能以数学语言给出这解答

• 这不是原因，注意前提是每层摔坏的几率相同

第二个再一个一个试，总可以在大约小于2*[sqrt(N)+0.5]次内找到

假设这样一个方案（实际上也没有别的方案）：

先选取一些节点A_0=1<A_1<A_2<……<A_k<A_{k+1}=N，用第一个包裹依次试验这些节点，得到M所在区间A_{s-1}<=M<A_s，然后再用第二个包裹在这个区间里一个个试上去。当M遍历1——>N时，需要的总次数为

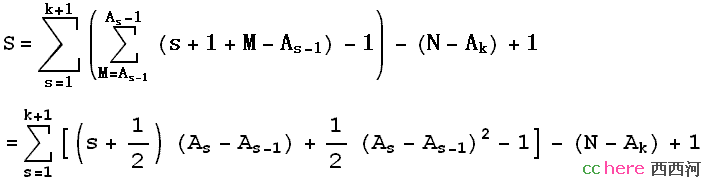
现在需要调整As和k的值使得S最小。先对As求偏导得到

2A_k=A_{k-1}+N

2A_s-A_{s+1}-A_{s-1}=1 1<s<k

2A_1=A_2+2

因此A_s=1+as-s^2/2，代入第一个方程（或者直接要求A_{k+1}=N也差不多）得到a=a(N,k)，把A_s和a代入S，得到S=S(N，k)，现在要找一个k使得S最小，对k求偏导并假设N非常大，即得k^2≈2N，S/N≈2k/3≈Sqrt(8N/9)

直接用等差数列（A_s=as+b）得到k^2≈N，S/N≈k≈Sqrt(N)。

• 这个式子不对

思路缓慢啊～～

现在再整理一下思路，当然是递减步长。

首先层数为N时，我们第一步长为S=sqrt(N)，在尝试后，问题简化为层数为N-S的问题了。

就很容易得到上述答案。

看来数学不好是不行。这样的问题我就是无法用数学语言说清楚！

看来我的直觉很烂

前面都是一样的，但是

这个通项公式似乎少了一点，好像应该是A_s=1+A_1*s-(s^2+s)/2

F1(x)= 有一个包裹时x层最少试验次数

F2(x)= 有两个包裹时x层最少试验次数

F1(x)=x

F2(x)= MIN(

1+MAX(F1(1),F2(x-2)),

1+MAX(F1(2),F2(x-3)),

...,

1+MAX(F1(x-2),F2(1)))

算一算

x F1 F2

1 1 1

2 2 2

3 3 2

4 4 3

5 5 3

6 6 3

7 7 4

8 8 4

...

F2 = 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, ....

通解：

F2(x)=n

n*(n-1)/2 < x <= (n+1)*n/2

最后一个不等式对自然数很好解。

F2(10) = 4

F2(100) = 14

F2(1000) = 45

换一个角度。 这个问题是在求：

填满一颗高度为n的二叉树， 并且每条从根到叶的路径最多只能经过一条左支。

问能填多少个节点？

x= (2^n-1) - ((2^(n-2)-1) + 2(2^(n-3)-1) + 3(2^(n-4)-1)+...+(n-2)(2-1))

= (2^n-1) - (2^n -n-2-(n-1)(n-2)/2)

= n(n-1)/2

同理可推广到， 有3个包裹的问题， 等效于填一颗高度n的二叉数， 每条从根到叶的路径最多只能经过两条左支。

有y个包裹的问题， 等效于填一颗高度n的二叉数， 每条从根到叶的路径最多只能经过y-1条左支。

谁知道 1^2 + 2^2 + 3^2 + ...+ n^2 这个序列怎么求和？

假设F（N，P）代表用P个包裹在最佳方案下的平均测试数

则显然

F（N，1）=（1+2+．．.+N)/N=(N+1)/2

如果包裹数大于层数则

F(N,P)=F(N,N)

F(2,2)=2

P大于1时

假设第一次包裹放在L层

F(N,P)=L/N*F(L-1,P-1)+F(N-L,P)*(N-L)/N

第一项代表第一次试验摔坏的情况,第二项代表未摔坏的情况

显然选取L使得上式最小时为最优

这样P=2时可以递归计算出最优解

n^3-(n-1)^3=3*n^2-3*n+1

理由是就是第一层不安全，你也只能放在第一层。

显然越高就越危险了。。。。

问题时初值如何办？

F(N,P)=Min{(L-1)*(1+F(L-1,P-1))/N+(1+F(N-L,P))*(N-L)/N} 你的表达式里缺了三个1，最后一个非常重要。（其实现在这个表达式也不全对，L=1，N时不成立，但是这不影响下面的分析，因为N很大时我们相信最小值不会在L=1或N时取到）

显然有F(N,P+1)<=F(N,P)…………………………………(1)

只考虑N>>1的情况。用归纳法证明F(N,P)∽A(P)N^B(P)，B(P)<=1，并求出A(P)，B(P)。

P=1时命题成立。现在假设F(N,P)∽A(P)N^B(P)成立，计算F(N,P+1)。可以合理地假设取到最小值的那个L满足1<<L<<N………………………(2)

把(1+F(L-1,P-1))*(L-1)/N+(1+F(N-L,P))*(N-L)/N对L/N展开，并考虑条件(1)，得

(1+F(L-1,P-1))*(L-1)/N+(1+F(N-L,P))*(N-L)/N

≈F(N,P+1)+1-L(F(N,P+1)+NF'(N,P+1))/N+A(P)/N*L^(B(P)+1)+无穷小量。

对L求导得到最小值，按定义这个最小值就是F(N,P+1)，也就是说

1-L(F(N,P+1)+NF'(N,P+1))/N+A(P)/N*L^(B(P)+1)的最小值必须是零。由此可以得到

F(N,P+1)+NF'(N,P+1)≈c*N^(B(P)/(1+B(P))，因此F(N,P+1)≈A(P+1)N^B(P+1)，

这里的B(P)=1/P，A(P)=P/(P+1)(P!)^(1/P)

当P趋于无穷大时A(P)≈(P-1)/e+Log[2πP]/(2e)。

L(P)∽N^(1-1/P)*P/(P!)^(1/P)

愿意的话可以进一步算得

F(N,P)=P/(P+1)(P!)^(1/P)*N^(1/P)+C(P)+o(1)

C(1)=1/2，C(P)=(P-2)/2，P>1

L(P)∽N^(1-1/P)*P/P!^(1/P)+D(P)+o(D(P))

D(P)=-N^(1-2/P)*P(P-1)/(P!)^(2/P)/2

可以把它们组合成更紧凑的形式L(P)∽E*(N-E/2*N^(1-1/P))^(1-1/P)

E=P/P!^(1/P)

实际值与近似值的差

P=2 F(N,2)-(Sqrt[8N/9]-4/3/Sqrt[N])

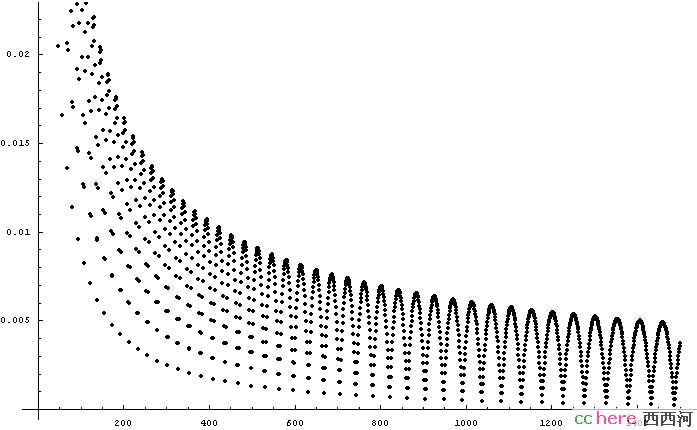
P=3 F(N,3)-((81N/32)^(1/3)+1/2)

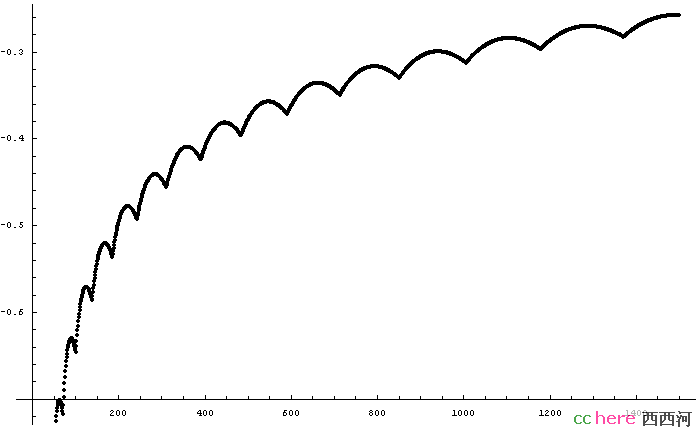
P=4 F(N,4)-((6144N/625)^(1/4)+1)

F(N，2)的进一步估计

F(N，2)≈(8N/9)^(1/2)-4/3/Sqrt[N]+Abs[Cos[πSqrt[2N]]]/(π(Sqrt[π N]-5))，最后一项分母里的常数不是太靠得住。

“量子化”条件：当Sqrt(2N)=n+1/2时估计式(8N/9)^(1/2)-4/3/Sqrt[N]的精确度特别高，此时L=n，当

Sqrt(2N)=n时精确度最差，此时L=n-1/2。

点：F(N,2)-(Sqrt[8N/9]-4/3/Sqrt[N])

红线：Abs[Cos[πSqrt[2N]]]/(π(Sqrt[π N]-5))

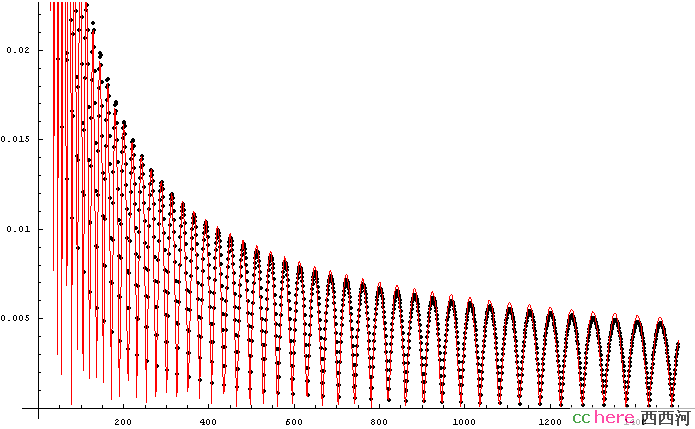
F(N，P)里总是有一些振荡现象，这是因为近似计算时总假设N，L为实数，但实际上它们只能是整

数。猜想这些振荡可以用Abs[Cos[πP(N/P!)^(1/P)+Pπ/2]]/N^(1/P)来很好地逼近。比较麻烦的是

F(N，P)的振荡会遗传给F(N，P+1)。这会使得寻找参数的难度变大。